소수란 무엇일까?
소수는 1보다 큰 자연수 중에서, 1과 자기 자신만을 약수로 가지는 수이다.
몇 개의 숫자를 가지고 생각해 보자.
1) 숫자 '1'은 소수가 될 수 없다.
2) 숫자 '2'는 1과 자기 자신(2) 만이 약수이므로 소수이다.
3) 숫자 '10'은 약수가 1, 2, 5, 10 이므로 소수가 아니다.
4) 숫자 '11'은 1과 자기 자신(11) 만이 약수이므로 소수이다.
1. 그렇다면, N이라는 숫자가 들어왔을 때 소수인지 아닌지를 판별하려면 어떻게 해야 할까?
가장 단순한 방법으로는, 숫자 2부터 N - 1에 도달할 때 까지 나누어 보는 것이다.
예를 들면, 숫자 '10'의 경우, 숫자 2가 10/2 = 5를 달성하므로, 소수가 아니다.
즉, 이를 코드로 작성하면 아래와 같다.
#include <iostream>
using namespace std;
bool isPrime(int number)
{
if (number < 2) return false;
for (int i = 2; i < number; i++)
{
// 1과 자기 자신이 아닌 수 중에서 자신과 나눴을 때, 나누어 떨어지는 수가 존재한다면
// 그 수는 소수이므로 빠른 Return 을 통해 소수임을 알린다.
if (number % i == 0) return false;
}
return true;
}
int main()
{
while (1)
{
int number;
cin >> number;
if (isPrime(number)) cout << number << "는 소수입니다.\n";
else cout << number << "는 소수가 아닙니다.\n";
}
}

다만 이렇게 구현하면 1부터 N까지의 수를 모두 확인해야 한다는 단점이 존재한다.
시간 복잡도가 O(N) 이 되므로, 조금 더 빠른 방법이 없을지 항상 생각해 보아야 한다.
2. 그렇다면, 더 빠른 방법은 뭐가 있을까?
우선은 약수의 성질에 대해서 조금 더 이해할 필요가 있다.
위의 방법 (1부터 N까지 약수를 구하는 방법) 한번 같이 숫자를 떠올리며 생각해 보자.
숫자 '10'을 예로 들어 보자.
10의 약수는 1, 2, 5, 10 이다.
숫자 '100'을 예로 들어 보자.
100의 약수는 1, 2, 4, 5, 10, 20, 25, 50, 100 이다.
숫자 '9999'를 예로 들어 보자.
9999의 약수는 1, 3, 9, 11, 33, 99, 101, 303, 909, 1111, 3333, 9999 이다.
어떤 공통점이 보이는가?
숫자 '100'으로 약수를 계산하는 과정을 떠올려 보자.
1은 100으로 나누어 떨어진다.
2는 50으로 나누어 떨어진다.
4는 25로 나누어 떨어진다.
5는 20으로 나누어 떨어진다.
10은 10으로 나누어 떨어진다.
20은 5로 나누어 떨어진다.
...
위의 과정에서, 우리는 숫자 '10'까지 계산한 이후부터는 뒤의 약수를 구할 필요가 없다는 것을 알고 있다.
이미 1~9를 지나오면서 그 뒤의 약수는 모두 앞에 나온 약수들과 짝지어짐을 알 수 있으며,
10*10 = 100 을 하면서, 더 이상 짝지어지는 약수가 나올 수 없음을 알 수 있다.
즉, 우리는 √N 까지만 약수를 구하면, 그 이후의 약수는 구할 필요가 없다는 것을 이해한 것이다.
이와 같은 사실을 기반으로, 1번의 코드를 아래와 같이 리팩토링 할 수 있다.
#include <iostream>
using namespace std;
bool isPrime(int number)
{
if (number < 2) return false;
// 사실 sqrt(number) 까지만 계산해도 문제가 없다!
for (int i = 2; i <= sqrt(number); i++)
{
if (number % i == 0) return false;
}
return true;
}
int main()
{
int number;
cin >> number;
if (isPrime(number)) cout << number << "는 소수입니다.\n";
else cout << number << "는 소수가 아닙니다.\n";
}
반복문의 조건을 √N - 1 까지로 바꿨을 뿐인데,
시간 복잡도는 O(N) 에서 O(√N) 으로 바뀌었다.
단순히, N까지 검사했던 것을 √N 까지 검사하는 것으로 변경했으므로, 시간 복잡도는 O(√N)이 된 것이다.

이렇게 우리가 얼마만큼 시간을 단축시켰는지 그래프로 한눈에 확인할 수 있다.
시간 복잡도를 생각하는 것이 이렇게 중요하다 !
3. 더!! 더 빠른거 주세요!!
예를 들어서 2~N까지 수 중에서, 소수만을 출력해야 하는 문제가 있다고 생각해 보자.
그렇다면, 우리가 방금까지 작성했던 저 코드를 그냥 2~N까지 반복하면 될 문제가 아닌가?
integer 범위 내의 수가 들어온다고 가정하고, 바로 아래와 같이 코드를 작성해 보자!
#include <iostream>
using namespace std;
bool isPrime(int number)
{
if (number < 2) return false;
for (int i = 2; i <= sqrt(number); i++)
{
if (number % i == 0) return false;
}
return true;
}
int main()
{
int number;
cin >> number;
// 2부터 number까지의 수가 소수인지 아닌지를 검사하는 알고리즘
for (int i = 2; i <= number; i++)
if (isPrime(i)) cout << i << '\n';
}

이 코드의 시간 복잡도는 얼마일까?
앞서, O(√N) 이었던 소수 판별 알고리즘을 2~N까지, 즉 N-1번 반복했지만 뭐 N이나 N-1이나 비슷하므로
결론적으로 O(N * √N) 만큼을 반복했다고 할 수 있다.
그러나, 아래에서 소개할 에라토스테네스의 체 알고리즘을 사용하면 훨씬 더 빠르게 구할 수 있다.
4. 에라토스테네스의 체
뭔.. 뭔 토스? 프로토스인가?
아니다. '에라토스테네스' 라는 아저씨 고대 그리스의 수학자가 고안해 낸 소수를 빠르게 찾는 방법이라고 한다.

우리가 생각해 낸 방식과 크게 다르지 않지만, 이를 메모이제이션 및 DP를 사용하여 더 빠르게 찾는 방법이다.
다만 그만큼 메모리를 잡아먹기 때문에, 적당한 범위의 수를 찾을때 사용하는 것이 좋다. 아래에서 더욱 상세히 설명한다.
메모이제이션이 뭐죠?
여기서 크게 중요한 것은 아니지만, 같은 계산을 또 또 또 하기는 싫으니까, 계산 결과를 저장해서 다음에는 같은 연산을 안해도 되게끔 캐싱하는 방법! 이라고 생각하면 좋다! 어려운거 아니다.
우리가 소수를 구하는 방법은 1과 자기 자신으로만 나누어 떨어지는 수를 계산하는 것이었다.
또한, 우리는 √N 까지만 계산하여 그 뒤의 약수는 구할 필요가 없다는 것도 생각해 내었다.
여기서 한발 더 나아가, 특정 범위 내의 소수를 모두 구하기 위해서 다음과 같은 생각을 할 수 있다.
만약, 우리가 특정 소수를 구했을 때, 그 소수의 배수는 과연 소수인가?
예를 들어서, 우리는 2가 소수라는 것을 알고 있다.
그런데 과연 2의 배수는 소수일까?
당연히, 아니다.
2의 배수를 바꾸어 말하면, 그 수는 2라는 약수를 갖고 있다 라는 의미가 된다. 그리고 이러한 수는 자신 외에도 약수가 존재하므로 소수가 아니다.
즉, 2부터 나아가며 그 수의 배수를 모두 배제한다면, 소수인지 아닌지 판별하는 알고리즘을 실행할 필요도 없어지는 것이다.

위 그림과 같이 배수를 모두 제외하면서, 그 수를 넘기며 계산하면 우리가 원래 했던 알고리즘보다 훨씬 빠르게 계산이 가능한 것이다.
너무 많이 하면 복잡하니까 딱 20까지만 해보자.
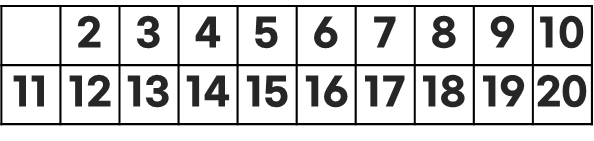
우선 2부터 시작하자.
2를 소수라고 가정하고, 2의 배수는 모두 제거한다.
어차피 2는 1을 제외하면 제일 작은 수 이므로 반드시 소수이다.
(자기 자신과 1 이외에는 나눌 수 있는 '수' 조차 없기 때문이다.)

다음은 3이다.
3 역시 2가 소수이고, 2의 배수가 아니므로 그보다 더 작은 수는 없다.
따라서 3은 소수인지 판별할 필요도 없이 그냥 소수인 것이다.
(마찬가지로, 2의 배수가 아니므로 자기 자신과 1 이외에는 나눌 수 있는 '수'가 없다.)

다음은 4 차례이지만, 4는 2의 배수로 표시가 되어있으므로 소수도 아닐 뿐더러 계산할 필요도 없다.
표시되지 않은 다음 수로 넘어간다.
여기까지 해서 사실상 √20 인 4.47213... 즉 4까지만 계산을 완료해도, 남아있는 수는 모두 소수이다.
왜냐하면 아까 2. 에서 언급했듯, 가장 큰 약수 짝을 지을 수 있는 부분은 그 수의 제곱근까지이며
그 뒤의 수 중에서 소수가 아닌 수는 모두 제곱근(4)보다 작은 수와 약수의 짝을 이뤄야 한다.
약수와 짝을 이룬다는 것은, 결국 그 약수의 배수라는 것이고
그렇기 때문에 제곱근 이상의 수들은 적어도 그보다 큰 약수를 가질 수는 없다!
근데 우리가 지금까지 배수들을 다 지웠으니까! 남은 수는 모두 소수인 것이다!
우리가 20까지의 수를 보고 있는 이상,
20의 제곱근 이상의 수, 예를 들어 5 이상의 약수를 갖기 위해서는
최소한 5*5=25 이상의 수여야지만 가능한데, 이는 이미 20을 넘는 수 이므로
다른 약수를 갖는 수가 현재 범위 내에서는 없다는 것이다!
그러므로 그 위의 수는 볼 필요도 없이 모두 소수인 것이다!
하지만 이해를 돕기 위해 일단 마무리는 지어 보자.
숫자 5도 2의 배수도 아니고 3의 배수도 아니었다.
나눌 수 있는 더 작은 수도 없으므로 5 역시 볼 것도 없이 소수이다.

쭊쭊 진행하면 우리는 제외된 부분을 생략하고 총 8개의 수만 검사하고도
20 이하의 소수를 모두 찾아낼 수가 있다!

이 흐름을 잘 따라왔다면 이해할 수 있을 것이다.
소수의 배수들을 모두 지우면서 이동하기 때문에, 해당 수가 소수인지 아닌지 계산할 필요도 없다는 것을!
이를 코드로 구현하면 아래와 같다.
#include <iostream>
using namespace std;
int main()
{
int number;
cin >> number;
// 1000이 들어온다면, 1001개만큼 할당해야 check[1000]에 접근이 가능하다.
bool* PrimeCheck = new bool[number + 1];
// 먼저, 모든 원소를 true 로 초기화해야 검사가 가능하다.
// 배수를 검사하며 이 true 원소들을 하나씩 하나씩 false 로 지울 것이다.
memset(PrimeCheck, true, (number + 1) * sizeof(bool));
// 0은 자연수가 아니고, 1은 소수가 아니다.
PrimeCheck[0] = PrimeCheck[1] = false;
for (int i = 2; i <= sqrt(number); i++)
// 만약 i가 그 누구의 배수도 아니었다면, 소수이므로
if (PrimeCheck[i])
{
// 그 소수의 배수를 모두 지워버린다.
for (int j = i * 2; j <= number; j += i)
{
PrimeCheck[j] = false;
}
}
// 저장된 결과 출력용
for (int i = 2; i <= number; i++)
if (PrimeCheck[i]) cout << i << " ";
}

100 이하의 소수를 잘 출력하는 것을 알 수 있다.
여기서는 단순하게 PrimeCheck 라는 배열을 만들어, 해당 숫자가 소수인지 아닌지 조사한 결과를 저장하고 있다.
이런 식으로, 탐색한 상태값을 저장하여 다음번 탐색에는 사용하지 않도록 하는 방식을 메모이제이션이라고 한다.
다만, 원래는 없던 bool 배열이 추가되면서 그만큼 메모리를 잡아먹게 된다는 단점이 있다.
따라서 실행 시간과 메모리 상황에 따라 판단 하에 사용해야 한다.
이제 다시 시간 복잡도를 한번 생각해 보자.
첫 번째 반복문에서 우리는 √N 만큼 루프를 반복하고,
i의 배수를 지우며 진행하는 내부 반복문에서는 앞서 설명했듯 결국 '소수'만을 남겨놓기 때문에
실제로는 '소수 수열'을 지나가며 검사하게 된다.
즉 알고리즘이 수행되는 순서가 2, 3, 5, 7, 11, 13 ... 이렇게 소수 수열에 대해서 실행되는 것이다.
이를 시간 복잡도 알고리즘으로 계산하면 점근적으로 log log N 에 근접한다고 한다.
이에 대해서는 아래 문서를 참고하면 된다.
https://en.wikipedia.org/wiki/Divergence_of_the_sum_of_the_reciprocals_of_the_primes
Divergence of the sum of the reciprocals of the primes - Wikipedia
From Wikipedia, the free encyclopedia Theorem The sum of the reciprocal of the primes increasing without bound. The x axis is in log scale, showing that the divergence is very slow. The red function is a lower bound that also diverges. The sum of the recip
en.wikipedia.org
이는 소수 수열을 오일러 증명, 폴 에르되시 증명과 테일러 급수를 가지고 설명하고 있다.
물론 난 무슨말인지 잘 모르겠다.
요컨대, 소수 수열은 log N (log log N) 에 수렴한다고 생각하면 될 것 같다.
결과적으로 시간 복잡도는 O (√N 그러나 일반적으로 N) * log log N 라고 할 수 있다.

즉, 그래프로 보면 이렇게나 시간을 줄일 수 있게 되는 것이다.
'알고리즘 > 수학' 카테고리의 다른 글
| 게임에서의 벡터와 내적, 그리고 외적 (1) | 2024.07.26 |
|---|
